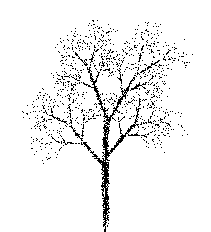
Iterated Function Systems (IFS) are an elegant way for generating fractal images. These problems address some background and applications of IFS.
In The Gasket Shall be our Guide we explore basic transformation properties of the Sierpinski gasket.
In Making Some Other Pictures we use some simple variations of the gasket rules to produce other fractals.
In Deterministic Iterated Function Systems we use the "deterministic algorithm" (at each step, apply all the transformations to every point of the picture) to generate a variety of fractal images.
In Random Iterated Function Systems we use the "random algorithm" (start with a point and apply the transformations one at a time, in random order, each time to the point produced by the previous application) to generate a variety of fractal images.
In Pictures from Nature we generalize the transformations, allowing for squashing and skewing to produce pictures more closely resembling natural objects.
In Collage Theorem Problems we consider "inverse problems:" starting with a fractal picture, how would we find the transformations to make that picture?
In Coloring we use transformations to assign "addresses" to regions of the fractal, and employ these addresses to color the picture.
In What is Random? we find what aspects of "random" are needed in the random algorithm.
Return to Exercises Introduction
Go to Chapter 1 exercises
Go to Chapter 3 exercises
Go to Chapter 4 exercises
Go to Chapter 5 exercises
Go to Chapter 6 exercises
Go to Chapter 7 exercises
Go to Chapter 8 exercises
Go to Chapter 9 exercises
Return to Chaos Under Control