
Driving an IFS by a text suffers from the lack of a canonical conversion of the text to a string of four symbols. For numerical sequences, the method of coarse-graining can be used. For texts, the corresponding approach of dividing the letters into bins inherits the arbitrariness of alphabetical ordering, while binning words by parts of speech may reflect more grammatical constraints than writer's style. Consequently, those experimenting with text-driven IFS must find a natural way of converting text into symbols.
In their project for the autumn, 2000, fractal geometry
course, Alexander Clark and Thao Tran evaluated sound patterns of texts,
with the goal of comparing the sonnets of Shakespeare and Wordsworth. Clark and
Tran used the soundex algorithm, a method of converting words into 5 digit "codes."
The first two digits of the code is determined by the first letter of the word,
according to the substitution
| letter | coded as |
| a,e,i,o,u,y,h,w | not coded |
| b,f,p,v | 1 |
| c,g,j,k,q,s,x,z | 2 |
| d,t | 3 |
| l | 4 |
| m,n | 5 |
| r | 6 |
After three digits have been assigned, the rest of the word is ignored; for short words, missing digits are filled in with 0s. Adjacent consonants from the same code group contribute only one digit, as do consonants from the same code group separated by w or h. Finally, ignore a consonant immediately following an initial letter from the same code group.
For example, the first line of Shakespeare's Sonnet 1
| From fairest creatures we desire increase |
| 16650, 16623, 13636, 33000, 14260, 19526 |
After converting the text into a sequence of 5 digit codes, Clark and Tran used the numerical coarse-graining method to drive the IFS. Here are the results for all of Shakespeare's sonnets (left) and all of Wordsworth's sonnets (right).

|
There is little visible pattern, except possibly a slight decrease in density along the Wordsworth diagonal. Most often, here the transformation associated with a word is determined by the alphabetic ordering of the first letter of the word. (This is why Clark and Tran called this the "primary structure" of the sonnets.)
Rhyme is determined by the end sounds of words, so Clark and Tran decided to investigate what they called the "secondary structure" of the texts. To make this fit most easily into the existing program, they inverted the order of the 5 digit code by placing the last three digits of the original code first. That is, the word "fairest" has primary code 16623 and secondary code 62316. To be sure, this secondary code does not reflect rhyme completely, but it is more sensitive to the end of the word. Coarse-graining the secondary codes and driving the IFS gave these pictures, Shakespeare on the left, Wordsworth on the right.
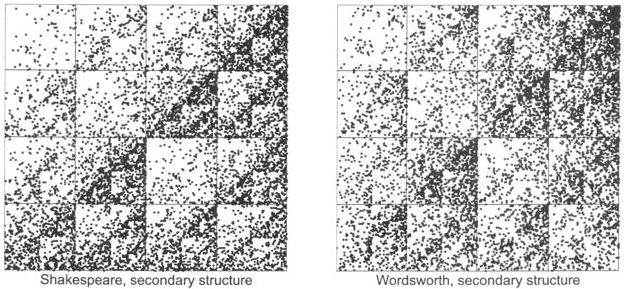
|
Clark and Tran speculate Shakespeare's driven IFS is more concentrated because Shakespeare's sonnets are in the form of three quatrains and a couplet, a structure that more easily supports repeating words than does Wordsworth's octave and sestet. Additionally, Wordsworth's sonnets involve more complete and complicated thoughts, hence more variation in words.
To test how much this pattern really represents the repetition of rhyming, Clark and Tran ran the driven IFS for the secondary structures of the first 10,000 words of War and Peace, of A Tale of Two Cities, and of the same length text made of several randomly selected writings. All revealed similar patterns.

|
Evidently, there are fewer words with secondary structure in bin 3. To see if this numerical difference alone is responsible for the gasket-like patterns, one could randomize the ordering of the words and drive the IFS with the corresponding secondary sequences. This test has not yet been done.
Return to Text Driven IFS