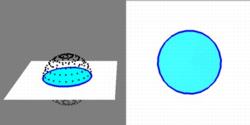
MPEG - 233K QuickTime - 171K GIF - 153K		A Square in Flatland can understand a sphere as a series of growing and shrinking circles over time. Here, time acts as the third dimension, but we recognize it as a third physical dimension. Note that the circle grows quickly at first, and slows down as the slice gets closer to the equatorial circle. The circles then begin to shink, slowly at first, then faster toward the end. Do you see why the rate changes?
MPEG - 90K QuickTime - 45K GIF - 330K		We could understand a visit from a hypersphere from the fourth dimension in the same way. We would see a small sphere appear and then grow. The rate of growth would start out fast, and then slow down as the slice of the hypersphere nears the "equatorial sphere". Once past the equator, the spheres begin to shink again, faster and faster until the sphere disappears as the hypersphere leaves our three-dimensional space again.