 |
The slices of a hypercube parallel to one of its cubical faces are themselves cubes. When we view the hypercube in orthographic projection straight at its face, the projection of the slice seems to stay in place (so I didn't make a movie of it, since nothing seems to happen). This is like the corresponding view of the face-first view of the cube sliced parallel to a face. | |

|
Here we slice the hypercube parallel to one of its square faces, and view it square first. The slice begins at the square that is farthest from our viewpoint (which is projected to the center of the figure). The slice begins to expand into a rectangular box. This corresponds to the cube slicing sequence starting at an edge, where we saw the slice begin as a line at the center and grow to a rectangle. As the slice progresses, the rectangular box expands into a wider and wider box until it reaches its maximum width. (Can you figure out how wide it is?) The slice is now half-way through the cube, and at this point the slice passes through 8 of the hypercube's vertices. After this, the box shrinks back to a square face, the one at the front of the hypercube, whose projection is again at the center of the figure. | |

|
This slicing sequence begins at an edge of the hypercube, and we view the hypercube in orthographic projection edge first. The closest and farthest edges both project to the central edge in the figure. As we begin to cut the hypercube, the slice becomes a triangular prism. This is because the (flattened) cubes at the top and bottom of the projected hypercube are beginning to be sliced corner first, and so these slices go through the triangle, truncated triangle, hexagon sequence. Meanwhile the other six cubes are sliced edge first, so go through the widening-shrinking rectangle sequence. This means that the slices of the complete hypercube are prisms. They start as triangular prisms, grow to larger triangular prisms, then as the slice reaches three more edges of the hypercube, the prisms become truncated, and eventually the sides become equal, forming a regular hexagonal prism. After this, the sequence reverses and shrinks back to the central edge. | |
|
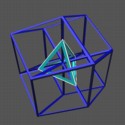
Finally, we slice the hypercube corner to corner. Our view is the one were we look directly at a corner, producing a figure in which all eight cubes are congruent shapes (correspinding to the view of the cube corner first so that it appears as a subdivided hexagon). The closest and farthest vertices are both projected to the central point of the shape, and the slices begin at this vertex. The initial slice is a tetrahedron at the center of the figure. Each face of the tetrahedron is a slice of one of the corners of one of the four cubes that meet at this vertex. As the slice progresses, these faces grow and eventually pass through four of the vertices of the hypercube. At this point, the corners of the tetrahedron begin to be cut off as the slice starts to pass through the other four cubes in the hypercube. Meanwhile the original triangular faces are beginning to form hexagons as they slice farther through the original four cubes. At a point half-way through these cubes (or one-third of the way through the complete hypercube), these four cubes are sliced by regular hexagons, and the complete slice forms the Archimedean solid known as the truncated tetrahedron. It has four regular hexagonal faces and four equilateral triangular faces. Further along, the hexagonal faces become more triangular again, and the small triangular faces grow larger. Half-way through the slicing sequence for the hypercube, all eight faces are equilateral triangles forming a Platonic sold, the octahedron. At this point, all eight of the cubes in the hypercube are sliced in exactly the same way. As the slice moves further, the sequence repeats itself, but in reverse; it passes through the truncated tetrahedron, then the tetrahedron, which again shrinks to the central vertex. Note that the final tetrahedron is inverted with respect to the one at the beginning of the slicing sequence. |