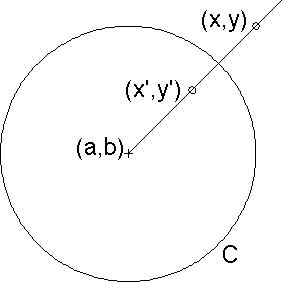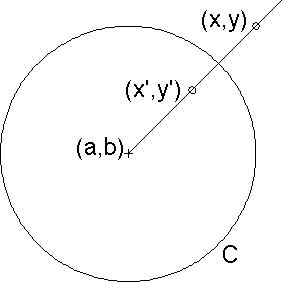
Fractals and Circle Inversions
Michael Frame, Barbara Bemis, Colleen Clancy, and Tatiana Cogevina
Inversion across a circle was introduced by Appolonious of Perga. Though
Appolonius' definition of inversion was synthetic, as was all geometry
at that time, we give an analytic characterization.
Starting with a circle C with center (a, b)
and radius r, and given a point (x, y), the point
(x', y') is the inverse of (x, y)
across the circle C if
-
Point (x', y') and point
(x, y) lie on the same ray from center
(a, b), and
-
The distance from the center to point (x, y)
multiplied by the distance from the center to point
(x', y') is equal to r2.
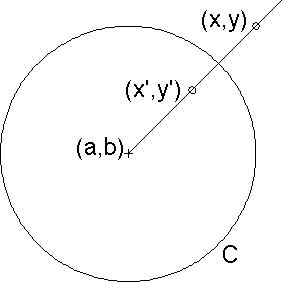
The points (x, y) and
(x', y') are inverses across the circle C.
Inversion in a circle has several properties
easily derived from the definition.
Continue to Inversion Limit Sets
Continue to Animations