Same Picture

First, fix a resolution, usually one pixel, to which the picture is to be rendered. Because all the IFS rules are contractions, the diameter of a region of address length N goes to 0 as N goes to infinity. (The "diameter" of a set is the maximum distance between any pair of points in the set. For example, the diameter of a circle is just the common notion of diameter; the diameter of a square is the diagonal length of the square.) Using the four transformations

T₁(x, y) = (x/2, y/2)

T₂(x, y) = (x/2, y/2) + (1/2, 0)

T₃(x, y) = (x/2, y/2) + (0, 1/2)

T₄(x, y) = (x/2, y/2) + (1/2, 1/2)

giving the unit square (see addresses), we see

diam(T_i(S)) = sqrt(2)/2

diam(T_jT_i(S)) = sqrt(2)/4

and in general

diam(T_{i_N}...T_i₁(S)) = sqrt(2)/(2^N)

Thus if we take N large enough that sqrt(2)/(2^N) < resolution, then the Random Algorithm will fill in the picture to the desired resolution if all regions of address length N are visited. Why should the Random Algorithm do this?

First, recall the Random Algorithm starts with the fixed point of one of the T_i. For definiteness, say we start with the fixed point (x₀, y₀) of T₁. The address of this point is 111... = 1^infinity. Suppose the first transformation applied is T_i₁. Then (x₁, y₁) = T_i₁(x₀, y₀) has address i₁111... = i₁(1^infinity). Continuing,

(x₂, y₂) = T_i₂(x₁, y₁) has address i₂i₁(1^infinity)

(x₃, y₃) = T_i₃(x₂, y₂) has address i₃i₂i₁(1^infinity)

...

(x_N, y_N) = T_{i_N}(x_N-1, y_N-1) has address i_N...i₂i₁(1^infinity)

(x_N+1, y_N+1) = T_{i_N+1}(x_N, y_N) has address i_N+1i_N...i₂i₁(1^infinity)

...

Keeping track of the regions of address length N visited by these points, we see

(x₀, y₀) belongs to the region with address 111...1 = 1^N

(x₁, y₁) belongs to the region with address i₁ 1^N-1

...

(x_N, y_N) belongs to the region with address i_N...i₂i₁

(x_N+1, y_N+1) belongs to the region with address i_N+1...i₃i₂

...

So we see each new transformation applied has this effect on the N-digit address: discards the right-most digit, shifts the remaining N-1 one place to the right, and inserts the new address on the left. If the transformations are applied randomly, then eventually every finite sequence of transformations will occur, and in particular, every sequence of length N will be applied. Consequently, every region with address length N will be visited by the (x_{i_k}, y_{i_k}). To the specified resolution, the Random Algorithm will generate the same picture as the Deterministic Algorithm.

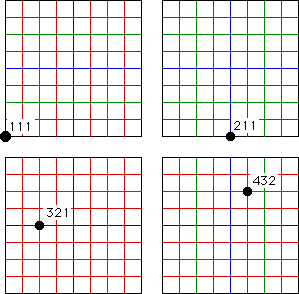
For example, suppose N=3 and we start with the point 1^infinity. To the specified resolution, this point lies in the region with address 111. If T₂ is the first transformation applied, the resulting point lies in the region with address 211. If T₃ and then T₄ are applied, the points lie in the regions with address 321 and 432. Continuing will fill in all the 4³ regions of address length 3.

Finally, note:

1. Using a random number generator is not the most efficient way to visit all regions of address length N. With some cleverness, specific orderings can be constructed to visit all regions more quickly.

2. Even in the limit of infiitely many applications, the Random Algorithm generates only countalbly many points, whereas the Determinisitc Algorithm typically produces an uncountable point set. For these methods to produce the same picture, we must modify the Random Algorithm by defining the set it produces to be the closure of the countable set.

3. For IFS with nonlinear transformations (e.g., Julia sets, circle inversion limit sets) the contraction factor varies with location, so under the Random Algorithm some regions may fill in very slowly indeed.

Return to Random IFS