Coarse-Graining the Data

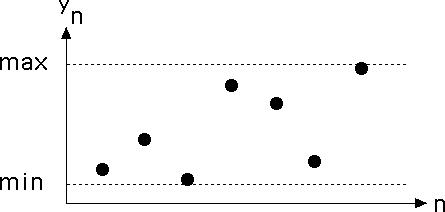
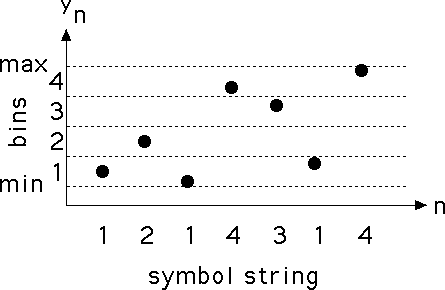
We turn the data into a sequence of 1s, 2s, 3s, and 4s. Suppose we have measured values x₁, x₂, ..., x_N. First, find the range of the values, that is, find the maximum (max) and the minimun (min) of the x_i.

Next, divide the range (min, max) into four equal-size bins, numbered 1, 2, 3, and 4. Each x_i lies in one of these bins, so we can convert the sequence x₁, x₂, ... into a sequence of 1s, 2s, 3s, and 4s, called the symbol string associated with the data. (We must make some choices if one of the x_i lands exactly on the between two bins. For example, we might always take the smaller bin number.)

Now we drive the IFS with the symbol string i₁, i₂, ..., i_N corresponding to the data sequence. Start with a point p₀ at the middle of the unit square. Then p₁ = T_i1(p₀), p₂ = T_i2(p₁), ..., and p_N = T_iN(p_N-1). To help visualize how the sequence is generated, note from the form of the T_i that

T₁(x, y) is the midpoint of the line from (x, y) to (0, 0),

T₂(x, y) is the midpoint of the line from (x, y) to (1, 0),

T₃(x, y) is the midpoint of the line from (x, y) to (0, 1), and

T₄(x, y) is the midpoint of the line from (x, y) to (1, 1).

Click on the small picture to see how the symbol string above drives the IFS.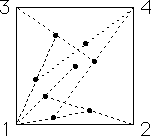

Return to Data-Driven IFS