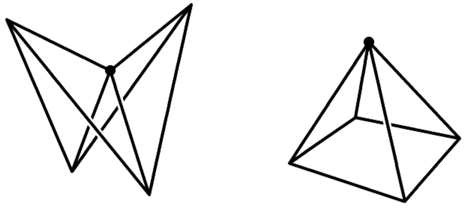
Polyhedral Tightness

The ideas of curvature can be extended to polyhedral surfaces as well, but we only care about its sign.

For smooth surfaces:

  • Positive curvature looks like a maximum for a height function
  • Negative curvature looks like a saddle.

For polyhedral surfaces:

  • Curvature is zero at every point other than the vertices
  • A vertex has negative curvature if it lies inside the convex hull of its neighbors
  • It has positive curvature if it lies outside.

[Prev][Up][Next]