A Bound on Total Absolute Curvature:
The total absolute curvature integral
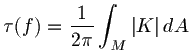
is closely related to the
total curvature integral, which is the integral over the
surface of the Gaussian curvature with respect to area. The
Gauss-Bonnet theorem gives a relation between the total curvature and
the Euler characteristic:
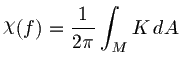
We can write these as follows
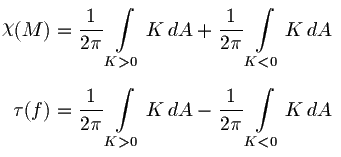
and then add to obtain
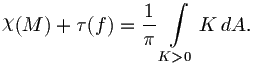
To evaluate the integral at the right, we break it into two parts, the
portion that is on the
convex envelope, H,
and the portion inside the convex envelope. Since both integrals are
positive, the second term can be dropped in the inequality:
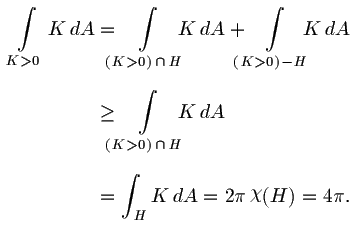
The equality for the last line comes from the following facts:
- Every point of H has non-negative curvature.
- If a point of M maps into H then it has
non-negative curvature.
- The points of H that are not in the image of M
have zero curvature. (If such a point had positive curvature, it would
have a small convex neighborhood not containing any point of M;
but this could be cut off making a smaller convex set containing
M, contradicting the fact that H is the convex envelope
of M.)
Finally, the integral can be evaluated in the last line since H
is convex, hence a topological sphere, so we can apply the
Gauss-Bonnet theorem.
Substituting this into the original formula yields the desired bound
on the total absolute curvature.
![[Right]](pix/Right.gif) Tightness and the convex hull
Tightness and the convex hull
![[Left]](pix/Left.gif) Tightness and its consequences
Tightness and its consequences
![[Up]](pix/Up.gif) Kuiper's original question
Kuiper's original question
![[TOC]](pix/TOC.gif)
![[Index]](pix/Index.gif)
![[Glossary]](pix/Glossary.gif)
![[Mail]](pix/Mail.gif)
![[Help]](pix/Help.gif)
7/21/94 dpvc@geom.umn.edu --
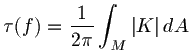
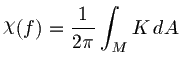
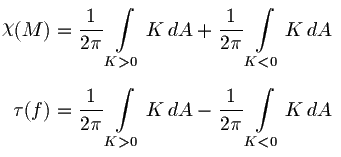
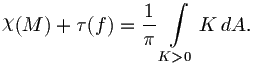
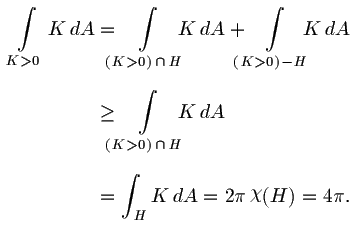
![[Right]](pix/Right.gif) Tightness and the convex hull
Tightness and the convex hull
![[Left]](pix/Left.gif) Tightness and its consequences
Tightness and its consequences
![[Up]](pix/Up.gif) Kuiper's original question
Kuiper's original question