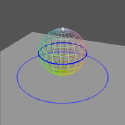
Stereographic projection maps the sphere (minus the north pole) to the plane. This is a one-to-one mapping that allows us to study the sphere by studying the plane instead. The idea is to point a light source at the north pole, and look at the shadows of points on the sphere as they appear on the plane below. In our movies below, the light is represented by a white sphere at the north pole, and the plane is the quite square below.
Note that points near the north pole are projected to points far away from the sphere (since the rays of light are nearly parallel to the plane). One important property of stereographic projection is that it maps circles on the sphere to circles in the plane, except for the circle that pass through the north pole, which are projected to lines in the plane below. The first movie shows the image of a circle as we rotate it on the sphere. As it rotates, the image gets larger and larger, until the circle passes through the north pole, when the image becomes a line. After this, the image closes again as a circle, but on the opposite side, and shrinks back down to its original size as the circle returns to its original position.
The second movie shows a band on the sphere rotating so that is passes through the projection point in a fashion similar to the circle in the first movie. As the band begins to rotate, the image of wthe portion that has moved closer to the light source enlarges and moves farther from the sphere, while the image of the part that moves toward the bottom of the sphere, and so farther from that light source, gets smaller. Note that as the band passes through the light source, its image extends out to infinity. After reconnecting on the other side, notice that the region of the plane that was outside the image of the band is now inside the band, and vice versa. (On the sphere, the region containing the light source has changed.)
|

|
The next movie takes the idea of stereographic projection to the fourth dimension. If we put a (four-dimensional) light source at the north pole of the three-sphere in four-space, we can project the three-sphere into three-space in exactly the same was that the two-sphere projects onto the plane. This is a one-to-one map, and allows us to understand the three-sphere by looking only at three-space.
As above, points near the light source are mapped points "near infinity", and point out near infinity are are close together on the three-sphere. Also, circles on the three-sphere map to circles (or straight lines) in three-space.
We have seen how the three-sphere can be divided into two congruent solid tori. The projection of the common boundary of these tori is shown in the movie below. Bands have been removed so that we can see its structure more easily. As we rotate the torus on the three-sphere, part of it moves closer to the light source, so its image enlarges and appears farther away, while part of it moves toward the south pole, so its image gets smaller. This distorted torus is called a cyclide of Dupin.
As the torus rotates through the light source in the fourth dimension, the image seems to extend out to infinity. (Like the circle in the first movie, this happens only at isolated points, not in an interval of points, like the band above.) Past this point, the image becomes a cylcide again, and what used to be outside is now inside; i.e. the torus as turned "inside out." As a result of this, the bands are now going around the torus "the other way." (Originally, they went around the hole in the torus, while now they go around the tube.)
As the torus continues to rotate, it passes through the light source again, so turns inside out once more. As the image returns to its original position, note that the colors are reversed (just as they were with the band above). We have gone through a 180-degree rotation, and so the torus has turned over. (Another 180 degrees would bring us back to the initial configuration.)
The last movie shows the image of the torus at the point when it has rotated to include the light source, so the image extends to infinity. This time, we use a checker-board pattern to make the surface appear more solid, while still being able to see through it. In this movie, we rotate the image in three-space (not in four-space), as a means of trying to better understand this interesting surface. Note that it divides three-space into two congruent regions (the images of the two solid tori that make up the three-sphere).

|

|