
This movie shows how projections of a cube can be made more understandable by looking at a sequence of images as the cube rotates above the plane of the projection. The various shadows make it clearer which parts are in front and which are behind.
We begin with a view of the 3D cube above the projection plane, with the light source above. The relation between the shadow and the rotating object is quite clear. After seeing the cube rotate, we move to a new viewpoint where all we can see is the shadow; we have to imagine the rotating cube from these 2D images.
The movies below investigate the rotation of a cube and of a hypercube in more detail.
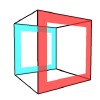
This movie shows the two-dimensional shadow of a cube as it rotates. Two of the faces are colored to help you follow how the shadow changes as the cube turns in space. At the start of the movie, the red square is closest to the light source (or viewer), and so it appears larger, while the blue face is farther away, and seems smaller. As the cube rotates, the blue square seems to shift to the side and both squares appear to become distorted. On the cube itself, they are still squares, but in the two-dimensional shadow, their images are trapezoids. As the cube rotates further, the blue square "pops" through the side of the red square, and eventually is completely outside it. The red square flattens out and "turns inside out" as we move from seeing one side of this face of the cube to seeing the other side. In a view of the cube where the red and blue faces are equally sized trapezoids, we see that these two faces are now the sides of the cube. As the cube turns further, the blue faces comes to the front, and is the largest square, while the red one moves to the back, and becomes smaller: the red and blue have interchanged positions. The rotation continues through the sequence again until the colored faces are back at the their starting positions.
We can easily reconstruct in our minds the three-dimensional cube from these two-dimensional pictures. The hard part is actually thinking of them as flat images! But this is what we have to do in order to make sense of the next movie, which shows the three-dimensional shadows of a hypercube rotating in four dimensions.
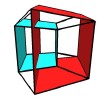
This movie shows the analogous three-dimensional shadows of the four-dimensional hypercube. Our initial view is of a large red cube containing a smaller blue one (some faces are removed to make it easier to see the interior structure). The red cube is closer to the light source (or the viewer), and so has a larger shadow. As the hypercube begins to rotate, the blue face moves to the side and both begin to become distorted as one side moves closer to the light and another farther away. At some point, the blue face passes through the side of the red one, and eventually pulls all the way through. The red cube begins to flatten out (as it becomes parallel to the viewing direction), and then appears to turn inside out, as the four-dimensional view moves from one side of the cube to othe other. At one point, the red and blue cubes form a symmetric view; each cube is now one of the sides of the hypercube and two different cubes are at the front and back. The rotation continues for another 90 degrees until the blue cube is at the front (largest) and the red one at the back (smallest). The sequence repeats itself with the colors interchanged as the blue cube moves again to the back. We end where we began, with a large red cube containing a small blue one.