4th Dimension Hcube-ortho: Hypercube Faces in Orthographic View

Hypercube Faces in Orthographic View

The movies below show the hypercube in orthographic projection. The initial (four-dimensional) viewpoint is looking directly at one of the cubical faces of the hypercube, so the projection appears to be a cube. The "front" and "back" cubes of the hypercube both appear to be the same size, and the remaining six cubes are projected "flat" as the faces of the cube. We then rotate our viewpoint to look directly at one of the square faces of the hypercube (the one at the center of the figure). This opens up two of the cubes that were flattened in the previous view (the orange and brown ones), and produces the analog of the "revolving door" illusion. Indeed, the four remaining flattened cubes are undergoing just that transformation in the last two movies.
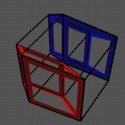
Our next rotation moves us to where we look directly at one of the hypercube's edges, again, the one at the center. Both the closest and the farthest edges appear at the same location in the projection, just as they do in a 3D cube viewed edge first. This rotation opens up two more of the cubes (the cyan and purple ones). Two of the cubes are still flat at the top and bottom, and we see them as the corner view of a 3D cube. The front corner is of each is attached to the front edge, while the back corner is attached to the back edge, but both appear at the same location in the projection. The remaining six cubes are formed by attaching corresponding faces of the two flattened cubes, and these six all are the same shape in the projection.
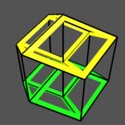
The final rotation in four-space brings our viewpoint to one that looks directly at a vertex of the hypercube. Here, both the closest and farthest vertex are seen at the center of the diagram, just as was the case witht he corner view of a 3D cube. This rotation opens up the last pair of cubes (the green and yellow ones) and now all eight cubes are projected as congruent shapes in three-space. This is the most symmetric view of the hypercube. The four cubes that share the front corner, when taken together, would fill up this three-dimensional shape, forming the "front" of the hypercube (just as the front three faces of a cube cover the entire hexagon of the corner view of a cube). Similarly, the other four cubes form the "back" of the hypercube, and they cover the shape a second time.
The four movies below show the same set of rotations, but with a different pair of cubes highlighted in each. These pairs are "opposite" cubes in the hypercube, as they have no face in common. One of them moving to the other woudl sweep out the entire hypercube.