|
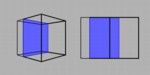
Here we see the sterographic and orthographic view of a cube looking directly at an edge of the cube while the cube is being sliced parallel to a face. The first sequence shows the slices if the face is one of the sides of the cube: it simply appears as a rectangle sliding through the projection. The second sequence shows the slices parallel to the top and bottom of the cube. Since these faces are parallel to our line of sight, the projections of the slices appear as line segments. |
|
|
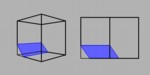
This movie shows the stereographic and orthographic view of a cube looking directly at an edge of the cube while the cube is being sliced starting at an edge. We begin at the bottom, back, left-hand edge and end at the top, front, right-hand one. In the projection, we see parallelograms growing, and then shrinking, but they actually are rectangular slices of the cube. A similar prgression would occur if we started at any of the top or bottom edges in the projection. In the second sequence, the slices starting at one of the side edges. Here, the slice is parallel to our line of sight, so the slice appears as a single line segment in the projection. The same would occur if we started at the right-hand edge. Finally, we slice the cube starting at the back edge. We see the slice as a thin rectangle growing wider and wider until it reaches two more edges of the cube parallel to our initial edge. At this point, the sides of the rectangle have swept out the back faces of the cube, while the top and bottom edges of the rectangle have swept out half of the top and bottom squares of the cube. From here, the rectangle shrinks again toward the front edge and disappears. The sides of the rectangle sweep out the front squares of the cube, while the top and bottom edges complete the top and bottom square faces of the cube. In the orthographic projection, the rectangle seems to grow out of the central edge and then shrink back to it again; but remember that both the front and the back edges are projected to this same location. Half way through, the slice is as wide as possible, forming a rectangle that has width equal to the diagonal of one of the cube. |
|
|
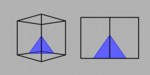
This movie shows the stereographic and orthographic view of a cube looking directly at an edge of the cube while the cube is being sliced starting at a corner. The first sequence shows the slices when we begin at one of the corners at either side. In the orthographic projection, all the slices appear as line segments, as our viewing direction is parallel to the slicing planes. When we begin at the lower back corner and end at the front top corner, we see triangles grow, and then get cut off as the slice passes three of the vertices of the cube. Half way through, there is a regular hexagon, and then the sequence reverses itself as the slice moves through the other half of the cube. Note that the equilateral triangles and regular hexagon look distorted due to the projection. Starting at the top back corner would look essentially the same. |