 |
|
Spheres Sliced in 2D and 3D
Flatlanders can understand a sphere as a sequence of circles changing over
time. The flatlanders see time as a third dimension, but we see the third
dimension as a physical one. Similarly, we can understand a hypersphere
from the fourth dimension as a sequence of spheres changing over time.
We use time as a means of representing a fourth physical dimension.
|
|
 |
|
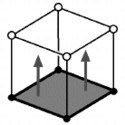
A Cube Falls Through Flatland
One way to show a three-dimensional cube to a Flatlander is to let the
cube pass through the plane of Flatland and see the sequence of shapes
that it produces. If the cube hits flatland face first, then the
Flatlanders will see a square appear, then remain for a while, and then
disappear. But this is not the only way a cube and pass through
flatland. Here we see three symmetric slicing sequences for the cube.
|
|
 |
|
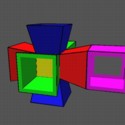
Hypercube Basics
These pages walk you through the analogs of the cube in lower and higher
dimensions, developing the sequence: point, line, square, cube, hypercube.
It begins the investigation of the hypercube by counting some of its parts,
and by locating the cubes that form the faces of the hypercube.
|
|
 |
|
Folding Cubes and Hypercubes
Here we look at how unfolding the square faces of a cube can help us to
explain a cube to Flatlanders. The shadows can be seen by the people in
Flatland, and they can try to use these shadows to interpret the folding
that we are doing in three-space. Similarly, we can unfold a hypercube
into three-space, and watch its shadow as it folds together in
four-space.
|
|
 |
|
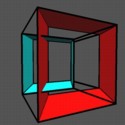
Orthographic and Perspective Projections
Our shadows of cubes and hypercubes have used stereographic projections, in
which things that are farther away appear smaller than things that are
nearby; but we can also use orthographic projection, which corresponds to
a viewpoint (or lightsource) that is "infinitely" far away. In this view,
far away things are not reduced in size. This makes our views more
symmetric, and reduces the picture to one that seems to be a
lower-dimensional one when our viewing direction is parallel to faces of
the cube or hypercube.
|
|
 |
|
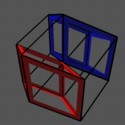
Rotating Cubes and Hypercubes
Rather than look at a single two-dimensional shadow of a cube, we can look
at a sequence of shadows as the cube rotates. This gives our
two-dimensional Flatlanders a better understanding of the cube as they
watch which pieces shrink (when they are far from the light) and which
grow (when they are near the light). We can readily interpret such
two-dimensional pictures as a three-dimensional cube rotating. Similarly,
we can look at a sequence of views of a hypercube as it rotates in
four-space.
|
|
 |
|
The Faces of the Hypercube in Orthographic Projection
On this page, we show the sequence of orthographic views of the hypercube
that we first introduced in the movies above, but this time, we highlight
various pairs of cubes, and track the changes that occur to them as we
move from viewpoint to viewpoint, first looking at a cubical face of the
hypercube, then a square face, then an edge, and finally a corner.
|
|
 |
|
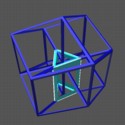
A Hypercube Falls Through Spaceland
These movies show the slicing sequences for the hypercube when it is sliced
cube first, square first, edge first, or corner first. These are the
analogous views to the slices of the cube passing through Flatland given
above. In each case, we view the hypercube from "above"; that is, the
square-first view is shown within the orthographic view of the hypercube
looking at it square first. You should be able to recognize the
similarities with three-dimensional cube slices, and may even see the
various cube-slicing sequences as the individual faces of the hypercube are
cut by the slicing hyperplane. The edge-first sequence is the first
interesting one, and you should be able to see the corner-first slicing of
the flattened cubes on top and bottom.
|
|
 |
|
Hypercube Slices Viewed Corner First
The previous set of movies show the four symmetric slicing sequences of the
hypercube, each viewed from a direction looking perpendicular to the
slicing hyperplane. Just as will the cube, however, we can view the
slices from different directions. The cube had three slicing directions
and three viewing directions, giving nine combinations in all; for the
hypercube, there are four of each, for sixteen all together. It seemed
excessive to produce this many, so we chose to show all four sequences from
one viewpoint, the corner view. In this view, all eight cubes are
visible, so we can see the entire slicing sequence clearly in each case.
|
|
 |
|
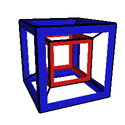
Hypercube Slices Colored by Cube
Here we show the slices of the hypercube viewed in orthographic projection
corner first, but this time we color the faces of the slices according to
which of the eight cubes of the hypercube they are slicing through. The goal here is to
see how the various faces of the slice sweep out the cubical faces of the
hypercube. You should be able to see the three slicing sequences of the
three-dimensional cube appear in different combinations in these movies.
|
|
 |
|
Stereographic Projections of Hypercube Slices
Our previous movies of the hypercube have almost all been in orthographic
projection. These movies show the slicing sequences of the hypercube in
stereographic projection, instead. Since in these stereographic views,
none of the cubes are flattened out, you can see how the faces of the
slices sweep out the cubes of the hypercube more easily. The edge-first
stereographic view of the hypercube is one you have not seen before.
|
|
 |
|
Interactive Models of 4-Dimensional Objects
It is not always easy to understand a 3-dimensional model from just one
view; it often helps to be able to walk around the object to see it from a
variety of viewpoint. All the more so when the 3-dimensional object is a
projection of an object from four dimensions. Many of the objects
illustrated in the links above are made available heres as 3D models that
can be rotated using a Java applet called JavaView.
|