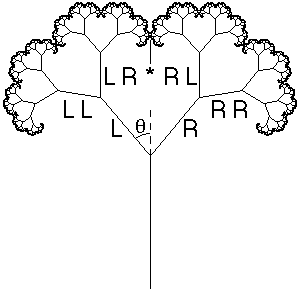
A binary fractal tree is defined recursively by symmetric binary branching. The trunk of length 1 splits into two branches of length r, each making an angle q with the direction of the trunk. Both of these branches divides into two branches of length r2, each making an angle q with the direction of its parent branch. Continuing in this way for infinitely many branchings, the tree is the set of branches, together with their limit points, called branch tips.
This study is an elaboration of Chapter 16 of [FGN].
In the obvious way, each branch is determined by a string of symbols L and R specifying the choice of direction taken along the tree to reach the branch. A branch determined by a string of n symbols has length rn; a branch tip is determined by an infinite string of symbols. Most of the analysis in [FT] results from converting eventually periodic symbol strings of branch tips into geometric series for the x and y coordinates of the branch tips, and making appropriate interpretations.
For example, in the tree on this page the branch tip marked * can be reached in two ways
LRRRRLRLRLRLRLR...and
RLLLLRLRLRLRLRL...
Consequently, for both sequences, the corresponding branch tips have x-coordinate 0. With simple trigonometry these sequences are converted into geometric series, giving r as a function of q. Details can be found in [FT].
Return to Introduction
Continue to Self-contacting scaling
Continue to Animations
Continue to References